December 09, 2019

Chapter 2 — Getting Started

2.1 Insertion sort

2.1-1

An illustration of the INSERTION-SORT procedure on the array $A=\left \langle 31, 41, 59, 26, 41, 58 \right \rangle$.

Insertion Sort Diagram

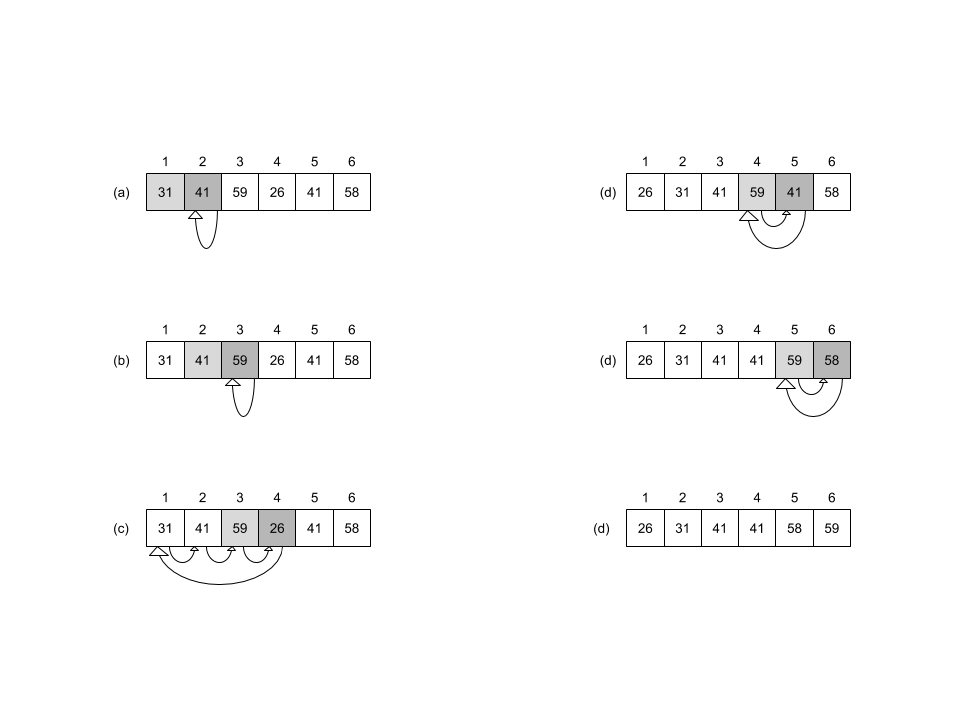
2.1-2

A version of INSERTION-SORT that sorts into nonincreasing order follows.

INSERTION-SORT(A)
for j = 2 to A.length
    key = A[j]
    i = j - 1
    while i > 0 and A[i] < key
        A[i + 1] = A[i]
        i = i - 1
    A[i + 1] = key

2.1-3

Consider the searching problem

Input: A sequence of n numbers A = 〈a₁, a₂, …, a_n〉 and a value v

Output: An index i such that v = A[i] or the special value NIL if v does not appear in A.

Below is pseudocode for linear search and a proof of correctness.

LINEAR-SEARCH(A,v)
for i = 1 to A.length
    if A[i] == v
        return i
return NIL

At the start of each iteration of the for loop, the subarray of items in $A$ up to but not including $i$ consists exclusively of elements that do not equal $v$.

Initialization: We start by showing that the loop invariant holds before the first loop iteration, when $i = 1$. The subarray of items in $A$ up to but not including $i$ is empty. Trivially, therefore, there is no element in the subarray matching $v$.

Maintenance: In lines 2-3 of the pseudocode, we check whether the element $A[i]$ is equal to v and return the index if that is the case. On the next iteration of the for loop, the subarray up to but not including the current value of $i$ will include the element from the previous iteration — otherwise the index would have been returned in line 3. Thus, the subarray consists only of elements that do not equal $v$.

Termination: The loop will terminate when $i > A.length = n$. Because each loop iteration increases $i$ by 1, we must have $i = n + 1$ at that time. The loop invariant for $i = n + 1$ states that the subarray of items up to but not including $n + 1$ consists exclusively of elements that do not equal $v$. Since this subarray is the entire array, we conclude that at the conclusion of the for loop, the entire array $A$ does not contain the value $v$, so returning NIL is the proper return value.

2.1-4

Consider the problem of adding two n-bit binary integers, stored in two n-element arrays $A$ and $B$. The sum of the two integers should be stored in binary form in an (n+1)-element array $C$. State the problem formally and write pseudocode for adding the two integers.

Input: n-element arrays A = 〉a₁, a₂, …, a_n〈 and B = 〉b₁, b₂, …, b_n〈 representing n-bit binary integers

Output: An (n+1)-element array C = 〉c₁, c₂, …, c_n〈 representing an (n+1)-bit integer, which is the sum of A and B.

SUM-BINARY-ARRAYS(A,B)
let C[1..n+1] be a new array
carry = 0
for i = 1 to A.length
    if A[i] == B[i]
        C[i] = carry
        carry = A[i]
    elseif carry == 1
        C[i] = 0
        carry = 1
    else
        C[i] = 1
        carry = 0
return C

2.2 Analyzing Algorithms

2.2-1

The function $n^3/1000 - 100n^2 - 100n + 3$ in Θ-notation is $\Theta (n^3)$.

2.2-2

Below is pseudocode for selection sort followed by an explanation of its loop invariant and further analysis.

SELECTION-SORT(A)
for i = 1 to A.length - 1
    let temp = A[i]
    let min = i
    for j = i + 1 to A.length
        if A[j] < A[min]
            min = j
    A[i] = A[min]
    A[min] = temp

Loop invariant: At the start of each iteration of the for loop, the subarray of items in $A$ up to but not including $i$ is sorted.

It only needs to run for the first $n - 1$ elements because if we were to run the loop again for $A.length$, the inner loop would be attempting to swap the element at $A[A.length]$ with the smallest element in the subarray $A[A.length..A.length]$, which is simply an array with the single element $A[A.length]$. An operation to swap $A[A.length]$ with $A[A.length]$ is unnecessary.

The best-case and worse-case running times of selection sort are both $\Theta (n^2)$. Regardless of whether the array is sorted initially, we must run $i$ for 1 to $A.length-1$ and $j$ from $i+1$ to $A.length$. This yields the summation placeholder. Removing the coefficients and lower-order terms, we arrive at n².

2.2-3

Let’s consider linear search again (see Exercise 2.1-3). On average, n/2 elements need to be checked, where n = A.length. In the worst case, n elements need to be checked.

LINEAR-SEARCH(A,v)	Average Case	Worst Case
for i = 1 to A.length	$n/2$	$n$
if A[i] == v	$n/2$	$n$
return i	1	1
return NIL	1	0

Average Case: $T(n) = n/2 + n/2 + 1 = n + 1$
Worst Case: $T(n) = n + n + 1 = 2n + 1$

Removing the coefficients and lower order terms, we arrive at a running time of $\Theta (n)$ for both the average-case and the worst-case.

2.2-4

We can modify almost any algorithm by first checking whether the input is already in the desired form. If it is, there is nothing more to do.

2.3 Designing Algorithms

2.3-1

An illustration of the operation of merge sort on the array $A = \left \langle 3, 41, 52, 26, 38, 57, 9, 49 \right \rangle$.

Merge Sort Diagram

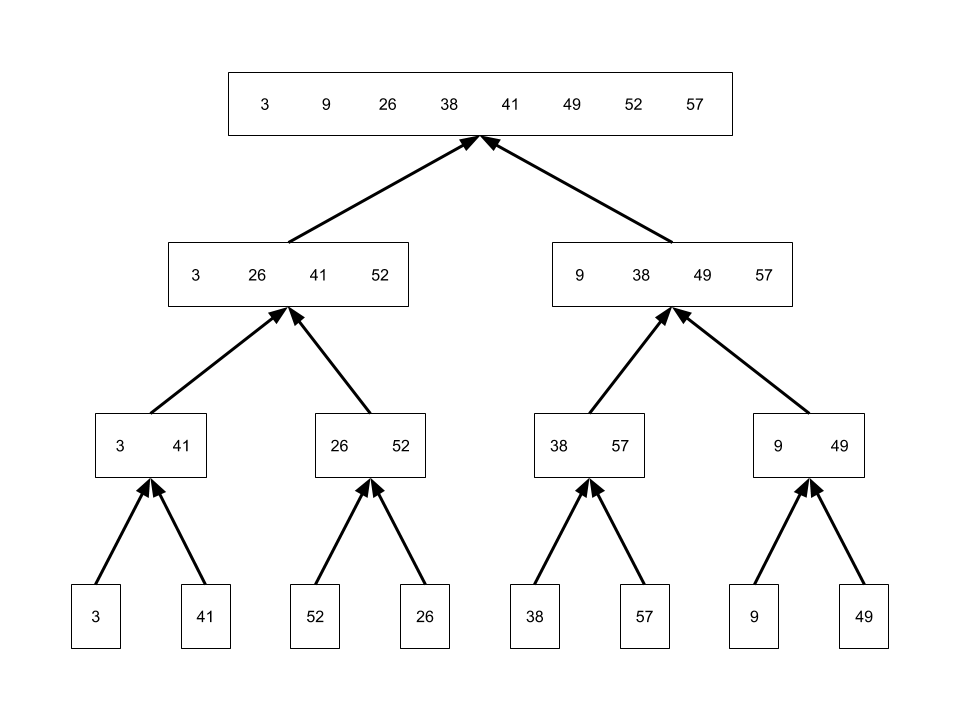
2.3-2

The rewritten MERGE procedure below does not use sentinels. Instead it copies the elements of $L$ and $R$, until one has all of its elements copied back into $A$. Then it copies the remainder of the other one back into $A$.

MERGE(A, p, q, r)
n1 = q - p + 1
n2 = r - q
let L[1..n1] and R[1..n2] be new arrays
for i = 1 to n1
    L[i] = A[p + i - 1]
for j = 1 to n2
    R[j] = A[q + j]
i = 1
j = 1
for k = p to r
    if i > n1
        A[k] = R[j]
        j = j + 1
    elseif j > n2
        A[k] = L[i]
        i = i + 1
    elseif L[i] <= R[j]
        A[k] = L[i]
        i = i + 1
    else
        A[k] = R[j]
        j = j + 1

2.3-3

We will show by mathematical induction that when n is an exact power of 2, the solution of the recurrence

$T(n) = \begin{cases} 2 & \text{ if } n = 2\\ 2T(n/2) + n & \text{ if } n = 2^k\text{, for } k > 1 \end{cases}$

is $T(n) = n\lg{n}$

Base case: $n=2$

$T(n) = 2$ by the recurrence above. This is equivalent to $T(2) = 2 \lg{2} = 2$.

Induction step

Assume true for $n = 2^k$. $T(2^k)=2^k\lg{2^k}=k2^k$.

Show true for $n = 2^{k+1}$.

$\begin{align*} T(2^{k+1}) &= 2T(\frac{2^{k+1}}{2}) + 2^{k+1}\\ &= 2T(2^k) + 2^{k+1}\\ &= 2[k(2^k)] + 2^{k+1}\\ &= k(2^{k+1}) + 2^{k+1}\\ &= 2^{k+1}(k+1)\\ &= 2^{k+1}(\lg{2^{k+1}})\\ &= n\lg{n} \text{, where }n = 2^{k+1} \end{align*}$

∴ We have shown that the recurrence above is true for values of $n$ where $n$ is an exact power of 2.

2.3-4

We can express insertion sort as a recursive procedure as follows. In order to sort $A[1..n]$, we recursively sort $A[1..n-1]$ and then insert $A[n]$ into the sorted array $A[1..n-1]$. In order to write a recurrence for the worst-case running time of a recursive version of insertion sort, we first analyze the worse-case running times of the divide, conquer, and combine steps.

Divide: The divide step simply computes the new subarray, $A[1..n-1]$, which takes constant time, $\Theta (1)$.

Conquer: We recursively sort the new subarray of size $n-1$, which contributes $T(n-1)$ to the running time.

Combine: To insert $A[n]$ into the sorted array takes $\Theta (n)$ time.

∴ The recurrence is $T(n) = T(n-1) + \Theta (n) + \Theta (1)$.

2.3-5

Below is pseudocode for binary search, in which we search a sorted array for $v$.

BINARY-SEARCH(A,v)
low = 1
high = A.length
while low < high
    mid = ⌊(low + high) / 2⌋
    if A[mid] = v
        return mid
    elseif A[mid] > v
        high = mid - 1
    else
        low = mid + 1

Lines 1-2 are each executed exactly once. Lines 3-10 have a worst-case running time of $\Theta (\lg{n})$, since the problem is divided in half with each iteration at line 4. This yields a runtime of $\Theta (\lg{n})$.

2.3-6

The insertion sort procedure in Section 2.1 cannot be improved using binary search to scan backward through the sorted subarray $A[1..j-1]$ because line 6 of the INSERTION-SORT procedure is responsible for shifting the elements greater than key into the proper place to make room for key in the sequence. This worst-case $\Theta (n)$ shift has to happen regardless.

2.3-7

Describe a $\Theta (n\lg{n})$-time algorithm that, given a set $S$ of $n$ integers and another integer $x$, determines whether or not there exist two elements in $S$ whose sum is $x$.

First, we transform set S into a sorted array $A$ in $\Theta (n\lg{n})$ time. Then we loop through each integer $a_k$ in $A$. On each iteration we perform a binary search through the rest of the array (the subarray $A[a_{k+1}..a_n]$), looking for an element $a_j$ such that $a_k + a_j = x$. A running time of $\Theta (n \lg{n})$ to sort the elements of set $S$ and a running time of $\Theta (n \lg{n})$ to scan the array for pairs of integers whose sum is $x$ yields a total running time of $\Theta (n\lg{n})$.

Problems

Check back later.

LINEAR-SEARCH(A,v)	Average Case	Worst Case
for i = 1 to A.length	\(n/2\)	\(n\)
if A[i] == v	\(n/2\)	\(n\)
return i	1	1
return NIL	1	0